Sketch the Graph of the Function $$f ( x ) = \log _ { 3 } ( x - 6 )$$

Multiple Choice

Sketch the graph of the function. Describe how the graph can be obtained from the graph of a basic logarithmic function.
- $$f ( x ) = \log _ { 3 } ( x - 6 )$$

A) Shift $y = \log _ { 3 } x$ right 6 units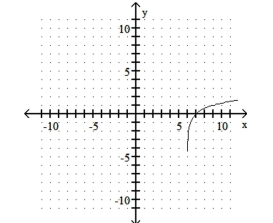

B) Shift $y = \log _ { 3 } x$ left 6 units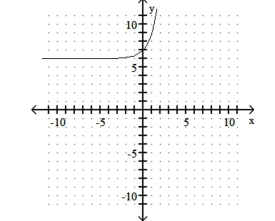

C) Shift $y = \log _ { 3 } x$ right 6 units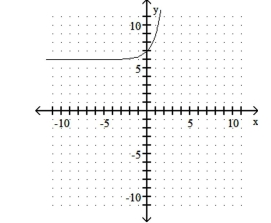

D) Shift $y = \log _ { 3 } x$ left 6 units