Multiple Choice
Match the equation to the correct graph.
-
A) 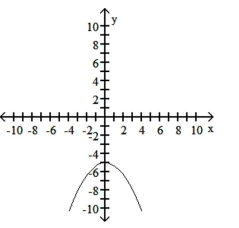
B) 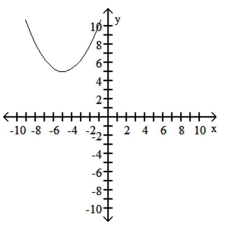
C) 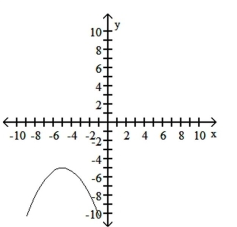
D) 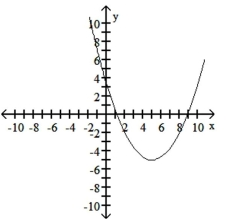
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q176: Solve.<br>- <span class="ql-formula" data-value="9 x ^
Q177: Solve.<br>- <span class="ql-formula" data-value="49 \mathrm {
Q178: Use the quadratic formula to find
Q179: Solve.<br>-A rock falls from a tower
Q180: Simplify. Write your answers in the
Q182: State whether the function is linear
Q183: Solve.<br>- <span class="ql-formula" data-value="\sqrt { 3
Q184: Use the quadratic formula to find
Q185: Simplify. Write your answer in the
Q186: Find the intervals on which the