Interpret the Slope and the Y-Intercept of the Least-Squares Regression $\mathrm { y } = \beta _ { 0 } + \beta _ { 1 } \mathrm { x }$

Multiple Choice

Interpret the Slope and the y-intercept of the Least-Squares Regression Line
-Civil engineers often use the straight-line equation, $\mathrm { y } = \beta _ { 0 } + \beta _ { 1 } \mathrm { x }$ , to model the relationship between the mean shear strength of masonry joints and precompression stress, $x$ . To test this theory, a series of stress tests were performed on solid bricks arranged in triplets and joined with mortar. The precompression stress was varied for each triplet and the ultimate shear load just before failure (called the shear strength) was recorded. The stress results for $\mathrm { n } = 7$ triplet tests is shown in the accompanying table followed by a SAS printout of the regression analysis.
$\begin{array}{l|lcccccc}\text { Triplet Test } & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\\hline \text { Shear Strength (tons) , } \mathrm{y} & 1.00 & 2.18 & 2.24 & 2.41 & 2.59 & 2.82 & 3.06 \\\hline \text { Precomp. Stress (tons) , } \mathrm{x} & 0 & 0.60 & 1.20 & 1.33 & 1.43 & 1.75 & 1.75\end{array}$





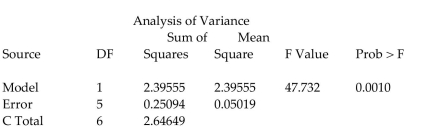
Give a practical interpretation of the estimate of the slope of the least squares line.

A) For every 1 ton increase in precompression stress, we estimate the shear strength of the joint to increase by $0.987$ ton.
B) For a triplet test with a precompression stress of 1 ton, we estimate the shear strength of the joint to be $0.987$ ton.
C) For every $0.987$ ton increase in precompression stress, we estimate the shear strength of the joint to increase by 1 ton.
D) For a triplet test with a precompression stress of 0 tons, we estimate the shear strength of the joint to be $1.19$ tons.