Solved

Graph the Function Using Transformations f(x)=−2x+3f ( x ) = \frac { - 2 } { x + 3 }

Question 144

Multiple Choice

Graph the function using transformations.
- f(x) =−2x+3f ( x ) = \frac { - 2 } { x + 3 }
Graph the function using transformations. - f ( x ) = \frac { - 2 } { x + 3 } A) B) C) D)


A)
Graph the function using transformations. - f ( x ) = \frac { - 2 } { x + 3 } A) B) C) D)
B)
Graph the function using transformations. - f ( x ) = \frac { - 2 } { x + 3 } A) B) C) D)
C)
Graph the function using transformations. - f ( x ) = \frac { - 2 } { x + 3 } A) B) C) D)
D)
Graph the function using transformations. - f ( x ) = \frac { - 2 } { x + 3 } A) 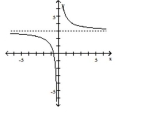B) 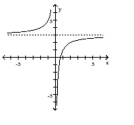C) 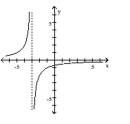D)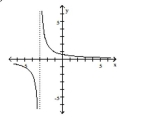

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q139: Graph the function.<br>- <span class="ql-formula" data-value="f

Q140: Write the equation of the function

Q141: Use the remainder theorem to find

Q142: State whether the function is a

Q143: Solve the problem.<br>-You have 80 feet

Q145: Use the Factor Theorem to determine

Q146: For the following rational function, identify

Q147: State whether the function is a polynomial

Q148: Use the graph of a power

Q149: Graph the function using transformations.<br>- <span