Multiple Choice
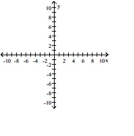
For the following rational function, identify the coordinates of all removable discontinuities and sketch the graph. Identify all intercepts and find the equations of all asymptotes.
- 
A) no removable discontinuities;
no -intercept, no -intercept;
asymptotes 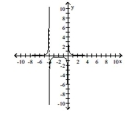
B) no removable discontinuities;
no -intercept, no -intercept;
asymptotes 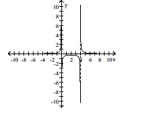
C) removable discontinuity at
no -intercept, no -intercept;
asymptote 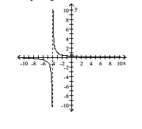
D) removable discontinuity at
no -intercept, no -intercept;
asymptotes 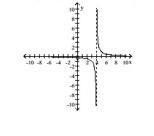
Correct Answer:

Verified
Correct Answer:
Verified
Q182: Find all complex zeros of the
Q183: Find the vertical asymptotes, if any,
Q184: Solve the variation problem.<br>-According to Ohm's law,
Q185: Use the quadratic function to determine
Q186: Use the end behavior of the graph
Q188: Use the graph of a power function
Q189: Form a polynomial f(x)with real coefficients
Q190: Use the intermediate value theorem to
Q191: Solve the variation problem.<br>-The distance that an
Q192: State whether the function is a