Multiple Choice
For the following rational function, identify the coordinates of all removable discontinuities and sketch the graph. Identify all intercepts and find the equations of all asymptotes.
- 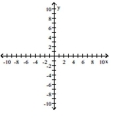
A) no removable discontinuities;
no \(\mathrm { x }\) -intercept, no \(\mathrm { y }\) -intercept
asymptotes \(x = 3 , x = 4 , y = 0\) 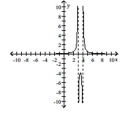
B) no removable discontinuities; no \(\mathrm { x }\) -intercept,
no \(\mathrm { y ; no \(x\) -intercept, no \(y\) -intercept;
asymptotes \(x = - 3 , x = - 4 , y = 0\) 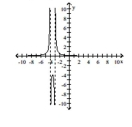
C) removable discontinuity at \(( - 4 , - 1 ) \) ;
no \(x\) -intercept, \(y\) -intercept: \(\left( 0 , \frac { 1 } { 3 } \right) \) ;
asymptotes \(x = - 3 , y = 0\) 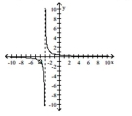
D) removable discontinuity at \(( 4,1 ) \) ;
no \(x\) -intercept, \(y\) -intercept: \(\left( 0 , - \frac { 1 } { 3 } \right) \)
asymptotes \(x = 3 , y = 0\) 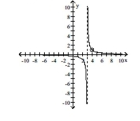
Correct Answer:

Verified
Correct Answer:
Verified
Q18: Use the graph of a power function
Q19: Find all complex zeros of the
Q20: Find the axis of symmetry of
Q21: Solve the problem.<br>-Consider the quadratic model
Q22: Use the rational zeros theorem to
Q24: First rewrite the quadratic function in
Q25: Use the Factor Theorem to determine
Q26: Find all complex zeros of the
Q27: Graph the quadratic function using its
Q28: Use the graph of a power