Multiple Choice
For the following rational function, identify the coordinates of all removable discontinuities and sketch the graph. Identify all intercepts and find the equations of all asymptotes.
- 
A) removable discontinuity at ;
-intercept: -intercept:
no asymptotes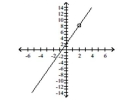
B) removable discontinuity at ;
x-intercept: , y-intercept: ;
no asymptotes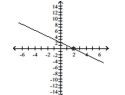
C) removable discontinuity at ;
-intercept: -intercept: ;
no asymptotes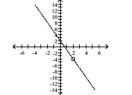
D) removable discontinuity at ;
-intercept: -intercept: ;
-intercept: -intercept: ;
no asymptotes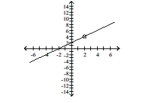
Correct Answer:

Verified
Correct Answer:
Verified
Q101: Graph the polynomial function.<br>- <span class="ql-formula"
Q102: Find the vertical asymptotes, if any,
Q103: Use the graph of a power function
Q104: Rewrite the quadratic function in standard
Q105: Find the x- and y-intercepts of
Q107: Graph the polynomial function.<br>- <span class="ql-formula"
Q108: Graph the polynomial function.<br>- <span class="ql-formula"
Q109: Graph the function.<br>- <span class="ql-formula" data-value="f(x)=\frac{x^{2}+4
Q110: Determine the possible number of positive
Q111: Solve the polynomial equation in the