Multiple Choice
Identify the graph of the function.
A) 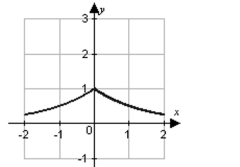
B) 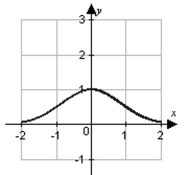
C) 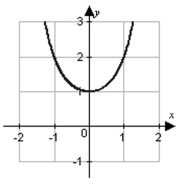
D) 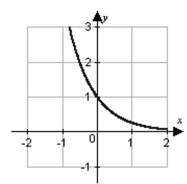
E) 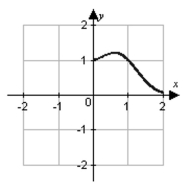
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q55: Simplify the expression <span class="ql-formula"
Q56: Solve the equation <span class="ql-formula"
Q57: Solve the exponential equation below algebraically.
Q58: Condense the expression <span class="ql-formula"
Q59: Simplify the expression <span class="ql-formula"
Q61: Find the exponential model <span
Q62: Condense the expression below to the
Q63: Solve the logarithmic equation below algebraically.
Q64: Simplify the expression <span class="ql-formula"
Q65: Solve the equation below algebraically. Round