Multiple Choice
Represent the complex number below graphically.
A) 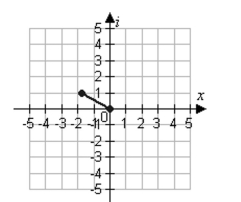
B) 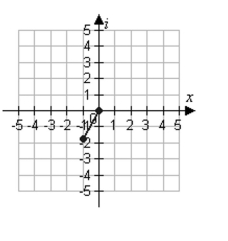
C) 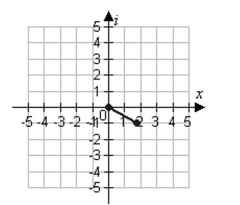
D) 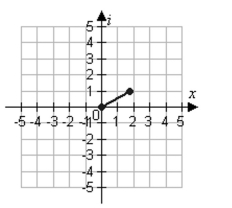
E) 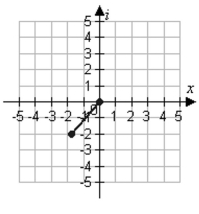
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q75: Perform the indicated operation using trigonometric
Q76: Use Heron's area formula to find
Q77: Given <span class="ql-formula" data-value="A =
Q78: Use DeMoivre's Theorem to find
Q79: Determine whether <span class="ql-formula" data-value="\mathbf
Q81: Given vectors <span class="ql-formula" data-value="\mathbf
Q82: Use DeMoivre's Theorem to find the
Q83: Find the component form of
Q84: In the figure below, <span
Q85: Find the trigonometric form of the