A Credit Card Company Operates Two Customer Service Centers: One

Multiple Choice

A credit card company operates two customer service centers: one in Boise and one in Richmond. Callers to the service centers dial a single number, and a computer program routs callers to the center having the fewest calls waiting. As part of a customer service review program, the credit card center would like to determine whether the average length of a call (not including hold time) is different between the two centers. The managers of the customer service centers are willing to assume that the populations of interest are normally distributed with equal variances. Suppose a random sample of phone calls to the two centers is selected and the following results are reported: 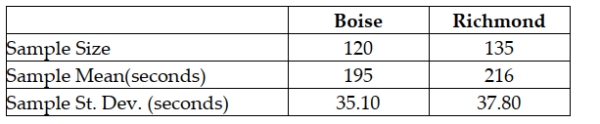Using the sample results, develop a 90% confidence interval estimate for the difference between the two population means.

A) -29.3124 ≤ (µ1 - µ2) ≤ -18.6876
B) -24.2412 ≤ (µ1 - µ2) ≤ -17.7588
C) -26.2941 ≤ (µ1 - µ2) ≤ -11.8059
D) -28.5709 ≤ (µ1 - µ2) ≤ -13.4291