Multiple Choice
Sketch the graph and show all local extrema and inflection points.
-y
A) Absolute maxima:
Inflection points: 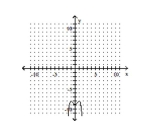
B) Absolute maxima:
Local minimum: No inflection points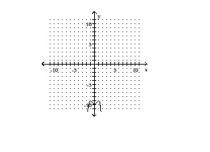
C) Absolute minima:
Inflection point: 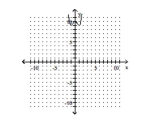
D) Absolute maxima: Local maximum: Local minimum:
Inflection points: 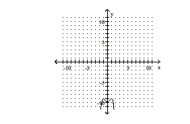
Correct Answer:

Verified
Correct Answer:
Verified
Q41: Determine whether the function satisfies the
Q42: Solve the problem.<br>-Given the acceleration, initial
Q43: Solve the problem.<br>-A trough is to
Q44: Solve the problem.<br>-Use Newton's method to
Q45: Estimate the limit by graphing the
Q47: Find the derivative at each critical
Q48: Find a value of c that
Q49: Sketch the graph and show all
Q50: Provide an appropriate response.<br>-Suppose that g(0) =
Q51: Find the extreme values of the