Multiple Choice
Parametric equations and and a parameter interval for the motion of a particle in the xy-plane are given. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph
traced by the particle and the direction of motion.
- 
A) ; Counterclockwise from to one rotation 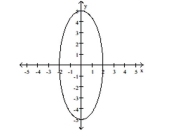
B) ; Counterclockwise from , to , one rotation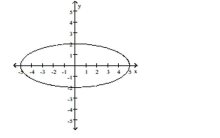
C) ; Counterclockwise from to , one rotation 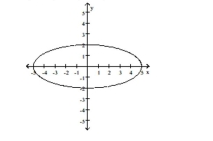
D) ; Counterclockwise from to , one rotation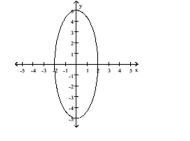
Correct Answer:

Verified
Correct Answer:
Verified
Q351: Solve the problem.<br>-Find the volume of
Q352: Find the length of the curve.<br>-
Q353: Sketch the region which is defined
Q354: Find the focus and directrix of
Q355: <span class="ql-formula" data-value="\text { Find the value
Q357: Graph the polar equation.<br>- <span class="ql-formula"
Q358: Find the standard-form equation for a
Q359: Find a Cartesian equation for the
Q360: Provide an appropriate response.<br>-Find the error
Q361: Provide an appropriate response.<br>-Which of the