Multiple Choice
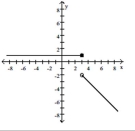
Find a formula for the function graphed.
-
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q54: Assume that f is an even function,
Q345: Find the domain and range for
Q346: Solve the problem.<br>-The accompanying figure shows
Q347: Determine whether or not the graph is
Q349: Is the function graphed below one-to-one?<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6591/.jpg"
Q351: Find the exact function value.<br>- <span
Q352: Determine an appropriate viewing window for
Q353: Solve for t or y, as
Q354: Graph the function. Determine the symmetry,
Q355: Find the inverse of the function.<br>-