Multiple Choice
Graph Hyperbolas Centered at the Origin
Use vertices and asymptotes to graph the hyperbola. Find the equations of the asymptotes.
- 
A) Asymptotes: 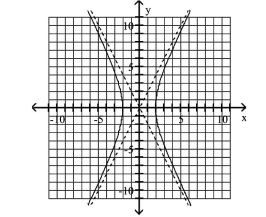
B) Asymptotes: 
C) Asymptotes: 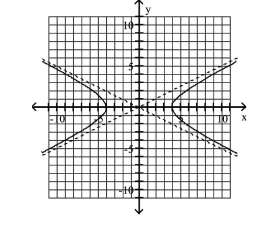
D) Asymptotes: 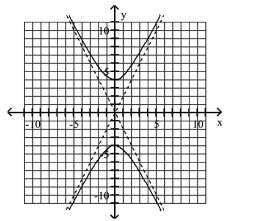
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q14: Graph Parabolas with Vertices Not at
Q15: Write Equations of Parabolas in Standard
Q16: Write Equations of Parabolas in Standard
Q17: Find the standard form of the
Q18: Graph Parabolas with Vertices Not at
Q20: Write Equations of Hyperbolas in Standard
Q21: Use the center, vertices, and asymptotes
Q22: Graph the parabola.<br>- <span class="ql-formula" data-value="x
Q23: Find the solution set for the
Q24: Convert the equation to the standard