Multiple Choice
Graph the function by making a table of coordinates.
- 
A) 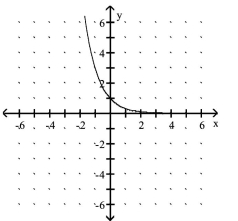
B) 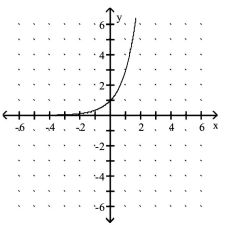
C) 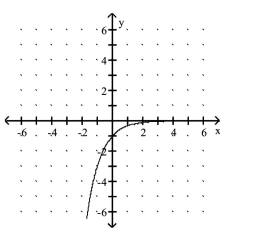
D) 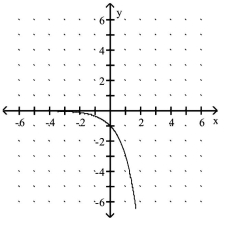
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q167: Write the equation in its equivalent
Q168: Use Natural Logarithms<br>Evaluate or simplify the
Q169: Use the Product Rule<br>Use properties of
Q170: Use properties of logarithms to condense
Q171: Use the Definition of a Logarithm
Q173: Solve the exponential equation. Use a
Q174: Model Exponential Growth and Decay<br>Solve.<br>-The value
Q175: Evaluate or simplify the expression without
Q176: Use Compound Interest Formulas<br>Use the compound
Q177: Model Exponential Growth and Decay<br>Solve.<br>-The half-life of