Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of 
A) 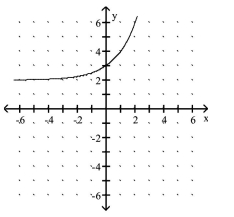
B) 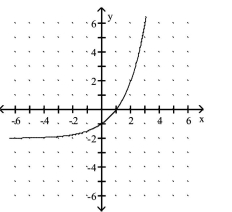
C) 
D) 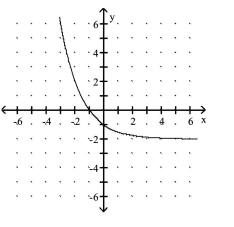
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q222: Use the Product Rule<br>Use properties of
Q223: Use the One-to-One Property of Logarithms
Q224: Solve the exponential equation. Express the
Q225: Use the Product Rule<br>Use properties of
Q226: Use Compound Interest Formulas<br>Use the compound
Q228: Write the equation in its equivalent
Q229: Solve the problem.<br>-The <span class="ql-formula"
Q230: Use common logarithms or natural logarithms
Q231: Solve the equation by expressing each
Q232: Write the equation in its equivalent