Multiple Choice
Solve the problem.
-A formula for the length of a diagonal from the upper corner of a box to the opposite lower corner is , where , and are the length, width, and height, respectively. Find the length of the diagonal of the box if the length is 20 inches, width is 14 inches, and height is 9 inches. Leave your answer in simplified radical form.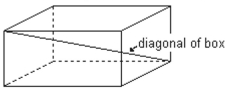
A) in.
B) .
C) in.
D) .
Correct Answer:

Verified
Correct Answer:
Verified
Q46: Solve Compound Inequalities<br>Solve the compound inequality.
Q47: Solve Linear Inequalities<br>Solve the linear inequality.
Q48: Solve the problem.<br>-A certain store has a
Q49: Recognize Identities, Conditional Equations, and Inconsistent Equations<br>Determine
Q50: Solve Linear Equations in One Variable<br>-6x
Q52: Solve Radical Equations<br>Solve the radical equation,
Q53: Solve the equation.<br>- <span class="ql-formula" data-value="\frac
Q54: Perform Operations with Square Roots of
Q55: Solve Quadratic Equations by the Square
Q56: Solve Linear Equations in One Variable<br>-