The Following MINITAB Output Presents a Multiple Regression Equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } +$

Multiple Choice

The following MINITAB output presents a multiple regression equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } +$ $+ b _ { 4 } x _ { 4 }$ .
The regression equation is
$$\mathrm { Y } = 5.3535 + 0.7929 \mathrm { X } 1 - 0.8918 \mathrm { X } 2 + 0.5297 \mathrm { X } 3 - 1.7948 \mathrm { X } 4$$
$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 5.3535 & 0.7240 & 0.8771 & 0.338 \\\text { X1 } & 0.7929 & 0.7986 & 3.3073 & 0.002 \\\text { X2 } & -0.8918 & 0.8208 & -2.9354 & 0.009 \\\text { X3 } & 0.5297 & 0.8980 & 1.9458 & 0.083 \\\text { X4 } & -1.7948 & 0.6461 & -1.0262 & 0.340\end{array}$



$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 1,188.8 & 297.2 & 7.7396 & 0.003 \\\text { Residual Error } & 31 & 1,190.1 & 38.4 & & \\\text { Total } & 35 & 2,378.9 & & & \\\hline\end{array}$
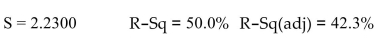
b₃x₃ What percentage of the variation in y is explained by the model?

A) 50.0%
B) 42.3%
C) 0.3%
D) 7.7396%