Solved

In Order to Justify the Construction of the Angle-Bisector

Question 373

Multiple Choice

In order to justify the construction of the angle-bisector 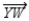In order to justify the construction of the angle-bisector of , we verify that two triangles are congruent by which method? A) SAS B) ASA C) SSS D) HL of In order to justify the construction of the angle-bisector of , we verify that two triangles are congruent by which method? A) SAS B) ASA C) SSS D) HL , we verify that two triangles are congruent by which method?


A) SAS
B) ASA
C) SSS
D) HL

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q368: For any quadrilateral with perpendicular diagonals of

Q369: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -In the figure,

Q370: What expression represents the exact circumference of

Q371: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -For

Q372: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -A right pyramid

Q374: A diagonal of a parallelogram separates the

Q375: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -A right circular

Q376: In kite HJKL, HJ = HL and

Q377: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt="Given that

Q378: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -If m