Essay
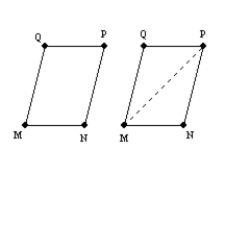
-Provide the missing statements abd nissing reasons for the proof of this theorem.
"If both pairs of opposite sides of a quadrilateral are congruent, the quadrilateral is a parallelogram."
Given: Quad. MNPQ;  and
and 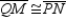 Prove: MNPQ is a parallelogram
Prove: MNPQ is a parallelogram
S1. R1. Given
S2. Draw diagonal 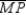 R2.
R2.
S3. R3. Identity
S4. R4. SSS
S5. 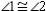 R5.
R5.
S6. R6. If 2 lines are cut by a trans. so that alternate interior angles
are congruent, these lines are parallel.
S7. 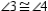 R7.
R7.
S8. 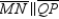 R8.
R8.
S9. R9.
Correct Answer:

Verified
S1. Quad. MNPQ;  and
and  R2. Thro...
R2. Thro...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q4: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide missing statements
Q5: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Given the rhombus
Q6: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide missing statements
Q7: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide missing statements
Q8: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide all statements
Q9: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Use the drawing
Q10: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Consider the drawing
Q11: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply all statements
Q12: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply missing statements
Q14: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply missing statements