The Following Scatterplot Shows the Percentage of the Vote a Candidate

Multiple Choice

The following scatterplot shows the percentage of the vote a candidate received in the 2004 senatorial elections according to the voter's income level based on an exit poll of voters conducted by CNN. The income levels 1-8 correspond to the following income classes: 1=Under $15,000; 2=$15-30,000; 3=$30-50,000; 4=$50-75,000; 5=$75-100,000; 6=$100-150,000;
7=$150-200,000; 8=$200,000 or more.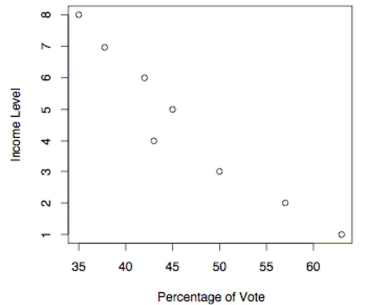
-Use the election scatterplot to determine whether there is a correlation between percentage of vote and income level at the 0.01 significance level with a null hypothesis of $Q _ { s } = 0$

A) The test statistic is not between the critical values, so we fail to reject the null hypothesis . There is no evidence to support a claim of correlation between percentage of vote and income level.
B) The test statistic is not between the critical values, so we reject the null hypothesis . There is sufficient evidence to support a claim of correlation between percentage of vote and income level.
C) The test statistic is between the critical values, so we reject the null hypothesis . There is sufficient evidence to support a claim of correlation between percentage of vote and income level.
D) The test statistic is between the critical values, so we fail to reject the null hypothesis . There is no evidence to support a claim of correlation between percentage of vote and income level.