Determine Whether the Statement Is True or False

Multiple Choice

Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​
The least-squares line must pass through at least one data point.

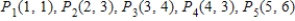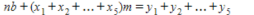
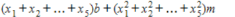
A) It is false. ​ Example. Find the least-squares line for the data ​ ​Solution. Here, we have n=5 and The least-squares line for the data is given by linear equation y= f(x) = mx+b where the constants m and b satisfy the normal equations 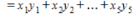Then, we obtain the normal equations 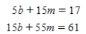Solving them, we found m=1, b=0.4 Therefore, the required least-squares line is y= x+0.4 The scatter diagram and the least-squares line are shown in the figure. We can see that the line does not pass through any data point.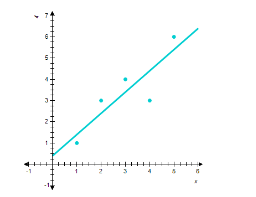

B) It is true, Suppose that we are given two data points 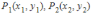If we try to fit a straight line to these data points, the line will miss the first and the second data points by the amounts d₁, d₂, respectively.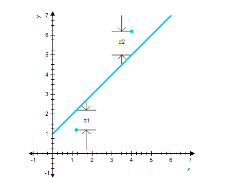

The principle of least squares states that the straight line L that fits the data points best is the one chosen by requiring that the sum of the squares be made as small as possible. But it is possible only in case when least-squares line passes through at least one data point.