Solved

Find the Critical Point(s) of the Function

Question 179

Multiple Choice

Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value: ​


A) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value: ; saddle point: Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value:
B) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value: ; relative maximum value: Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value:
C) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: B) ; relative maximum value: C) ; relative minimum value: ; relative minimum value: Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) ; saddle point: 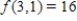B) 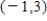; relative maximum value: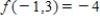 C) 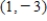; relative minimum value: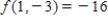

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q174: Use a double integral to find the

Q175: Find the average value of the given

Q176: Find the total differential of the function.<br>​

Q177: If it is true, explain why it

Q178: The Company requires that its corned beef

Q180: Maximize the function<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize the

Q181: In a survey it was determined that

Q182: The Ross-Simons Company has a monthly advertising

Q183: Find the average value of the given

Q184: Evaluate the double integral ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg"