Solved

Find the Critical Point(s) of the Function

Question 156

Multiple Choice

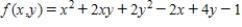
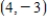Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) is the point of maximum, 11 is the relative maximum B) is the critical point, it is impossible to determine the relative extrema of the function C) is the point of minimum, -11 is the relative minimum D) is the critical point, the function has neither a relative maximum nor a relative minimum at this point E) no critical points ​


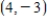A) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) is the point of maximum, 11 is the relative maximum B) is the critical point, it is impossible to determine the relative extrema of the function C) is the point of minimum, -11 is the relative minimum D) is the critical point, the function has neither a relative maximum nor a relative minimum at this point E) no critical points is the point of maximum, 11 is the relative maximum
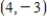B) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) is the point of maximum, 11 is the relative maximum B) is the critical point, it is impossible to determine the relative extrema of the function C) is the point of minimum, -11 is the relative minimum D) is the critical point, the function has neither a relative maximum nor a relative minimum at this point E) no critical points is the critical point, it is impossible to determine the relative extrema of the function
C) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) is the point of maximum, 11 is the relative maximum B) is the critical point, it is impossible to determine the relative extrema of the function C) is the point of minimum, -11 is the relative minimum D) is the critical point, the function has neither a relative maximum nor a relative minimum at this point E) no critical points is the point of minimum, -11 is the relative minimum
D) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) is the point of maximum, 11 is the relative maximum B) is the critical point, it is impossible to determine the relative extrema of the function C) is the point of minimum, -11 is the relative minimum D) is the critical point, the function has neither a relative maximum nor a relative minimum at this point E) no critical points is the critical point, the function has neither a relative maximum nor a relative minimum at this point
E) no critical points

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q151: Postal regulations specify that the combined length

Q152: Find the critical point(s) of the function.

Q153: Sketch the level curves of the function

Q154: Find the total differential of the function.

Q155: The total weekly revenue (in dollars) of

Q157: The population density of a certain city

Q158: Use a double integral to find the

Q159: Determine whether the statement is true or

Q160: Find the critical point(s) of the function.

Q161: Find the critical point(s) of the function.