Multiple Choice
An open rectangular box having a volume of 4in3 is to be constructed from a tin sheet. Find the dimensions of such a box if the amount of material used in its construction is to be minimal. Hint: Let the dimensions of the box be x by y by z. Then, xyz = 108 and the amount of material used is given by S = xy + 2yz + 2xz. Show that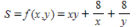 
Minimize f(x, y)
A) x = 1; y = 1; z = 2
B) x = 2; y = 2; z = 1
C) x = 2; y = 1; z = 1
D) x = 2; y = 1; z = 2
Correct Answer:
Verified
Correct Answer:
Verified
Q55: Minimize the function<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Minimize the
Q56: Use a double integral to find the
Q57: Evaluate the double integral<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate
Q58: The volume of a cylindrical tank of
Q59: Find the first partial derivatives of the
Q61: Find the average value of the function
Q62: Find the critical point(s) of the function.
Q63: Use a double integral to find the
Q64: Evaluate the first partial derivatives of the
Q65: Determine whether the statement is true or