Multiple Choice
Postal regulations specify that the combined length and girth of a parcel sent by parcel post may not exceed 120 in. Find the dimensions of the rectangular package that would have the greatest possible volume under these regulations. (Hint: Let the dimensions of the box be x'' by y'' by z'' (see the figure below) . Then, 2x + 2x + y= 120 , and the volume V=xyz. So that  . Maximize f(x,z) .)
. Maximize f(x,z) .) 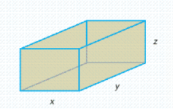
A) x = 20 inches, y = 40 inches, z = 20 inches, V = 16,000 cubic inches
B) x = 20 inches, y = 20 inches, z = 17 inches, V = 6,800 cubic inches
C) x = 22 inches, y = 40 inches, z = 22 inches, V = 16,000 cubic inches
D) x = 22 inches, y = 39 inches, z = 17 inches, V = 14,586 cubic inches
E) x = 22 inches, y = 40 inches, z = 17 inches, V = 14,586 cubic inches
Correct Answer:

Verified
Correct Answer:
Verified
Q141: An auxiliary electric power station will serve
Q142: Find the volume of the solid bounded
Q143: Maximize the function<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize the
Q144: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg"
Q145: The Company requires that its corned beef
Q147: Find an equation of the least-squares line
Q148: Find the first partial derivatives of the
Q149: Evaluate the first partial derivatives of the
Q150: Find the total differential of the function.<br>
Q151: Postal regulations specify that the combined length