Solved

The Volume V (In Liters) of a Certain Mass of Gas

Question 44

Multiple Choice

The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​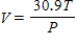 The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ ​
Compute The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ and The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ when T = 260 and P = 700.
​


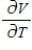A) The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​
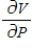B) The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​
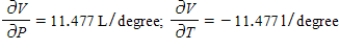C) The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​
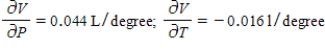D) ​ The volume V (in liters) of a certain mass of gas is related to its pressure P (in millimeters of mercury) and its temperature T (in degrees Kelvin) by the law ​ ​ Compute and when T = 260 and P = 700. ​ A) The volume increases by 0.044 L when the temperature decreases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ B) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume decreases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ C) The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​ D) ​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. 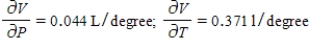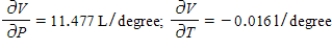​ The volume increases by 0.044 L when the temperature increases by 1 degree (beyond 260 K) and the pressure is fixed at 700 mm of mercury. The volume increases by 0.016 L when the pressure increases by 1 mm of mercury (beyond 700 mm) and the temperature is fixed at 260 K. ​

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q39: Use a double integral to find the

Q40: Maximize the function<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize the

Q41: Find the first partial derivatives of the

Q42: ​Find the approximate change in z when

Q43: Minimize the function ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Minimize

Q45: Find the second-order partial derivatives of the

Q46: Use a double integral to find the

Q47: Use a double integral to find the

Q48: Find the volume of the solid bounded

Q49: Find the critical point(s) of the function.