Solved

Find the Volume of the Solid of Revolution Obtained by Revolving

Question 51

Short Answer

Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve
​ Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve ​ ​ and below by the curve ​ ​ from to about the -axis. ​
and below by the curve
​ Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve ​ ​ and below by the curve ​ ​ from to about the -axis. ​
from Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve ​ ​ and below by the curve ​ ​ from to about the -axis. to Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve ​ ​ and below by the curve ​ ​ from to about the -axis. about the Find the volume of the solid of revolution obtained by revolving the region bounded above by the curve ​ ​ and below by the curve ​ ​ from to 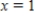about the -axis. -axis.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q46: Use the trapezoidal rule and Simpson's rule

Q47: Evaluate the definite integral by using the

Q48: The commissioner of the City of Newton

Q49: Find the indefinite integral. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg"

Q50: Approximate the value of the definite integral.<br>​

Q52: Use the trapezoidal rule and Simpson's rule

Q53: Find the volume of the solid of

Q54: Find the area of the region under

Q55: Evaluate the following improper integral whenever it

Q56: Find the indefinite integral.<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Find