Solved

By Computing the Volume of the Solid of Revolution Obtained

Question 140

Short Answer

By computing the volume of the solid of revolution obtained by revolving the region under the semicircle
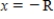​ By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. ​
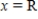from By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. to By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. about the By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. 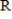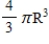-axis, show that the volume of a sphere of radius By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. is By computing the volume of the solid of revolution obtained by revolving the region under the semicircle ​ ​ from to about the -axis, show that the volume of a sphere of radius is cubic units. cubic units.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q135: Find the area of the region under

Q136: Use the table of integrals to find

Q137: Use the table of integrals to find

Q138: Evaluate the following improper integral whenever it

Q139: Evaluate the following improper integral whenever it

Q141: Find the area of the region under

Q142: Use the trapezoidal rule and Simpson's rule

Q143: Find a bound on the error in

Q144: The management of AstroWorld ("The Amusement Park

Q145: Find the indefinite integral. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg"