Solved

Find a Bound on the Error in Approximating the Given

Question 69

Multiple Choice

Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​ ​


A) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
B) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
C) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
D) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​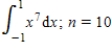 ​ A) 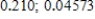B) ​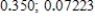 C) ​ D) ​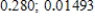

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q64: Use the trapezoidal rule and Simpson's rule

Q65: Use the table of integrals to find

Q66: Simpson's rule is more accurate than the

Q67: Use the formula ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Use

Q68: Use the table of integrals to find

Q70: Find the volume of the solid of

Q71: Evaluate the following improper integral whenever it

Q72: Find the volume of the solid of

Q73: Thanks to smaller and more fuel-efficient models,

Q74: Use the trapezoidal rule and Simpson's rule