Solved

Find a Bound on the Error in Approximating the Given

Question 58

Multiple Choice

Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​ ​


A) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
B) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
C) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​ ​ A) B) ​ C) ​ D) ​
D) ​ Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. ​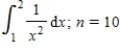 ​ A) 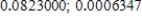B) ​ C) ​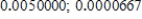 D) ​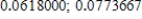

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q53: Find the volume of the solid of

Q54: Find the area of the region under

Q55: Evaluate the following improper integral whenever it

Q56: Find the indefinite integral.<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Find

Q57: Find a bound on the error in

Q59: Find the volume of the solid of

Q60: In a study conducted by a certain

Q61: Tracy purchased a 15-year franchise for a

Q62: Evaluate the improper integral whenever it is

Q63: Approximate the value of the definite integral.<br>​