Determine Whether the Statement Is True or False

Multiple Choice

Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​
If f and g are integrable, then .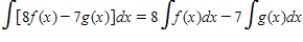
​

A) False. The indefinite integral of a difference of two integrable functions is not equal to the difference of their indefinite integrals. The indefinite integral of a constant multiple of a function is equal to the constant multiple of the indefinite integral of the function.
B) True. The indefinite integral of a difference of two integrable functions is equal to the difference of their indefinite integrals. The indefinite integral of a constant multiple of a function is equal to the constant multiple of the indefinite integral of the function.