Solved

Determine Whether the Statement Is True or False

Question 53

Multiple Choice

Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​
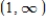The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. 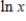is continuous on Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. .
​


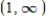A) The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. 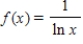is continuous and nonzero on Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. 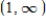, then the function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. 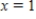is continuous in Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. , so the statement is true.
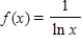B) The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. 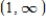is continuous but zero when Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. , then the function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. is not continuous in Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. ​ The function is continuous on . ​ A) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. B) The function is continuous but zero when , then the function is not continuous in , so the statement is false. , so the statement is false.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q48: ​Express the equation in logarithmic form.<br>​ <img

Q49: Use the definition of a logarithm to

Q50: Find the derivative of the function.<br>​ <img

Q51: Evaluate the expression. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate

Q52: Find the derivative of the function.<br>​ <img

Q54: Use logarithmic differentiation to find the derivative

Q55: ​Express the equation in logarithmic form. ​

Q56: Find the derivative of the function. ​

Q57: Find the derivative of the function. ​

Q58: Use the facts that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Use