Solved

By Cutting Away Identical Squares from Each Corner of a Rectangular

Question 9

Multiple Choice

By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​


A) By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​ A) B) C) ​ D) ​ E) ​
B) By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​ A) B) C) ​ D) ​ E) ​
C) ​ By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​ A) B) C) ​ D) ​ E) ​
D) ​ By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​ A) B) C) ​ D) ​ E) ​
E) ​ By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. ​ A) 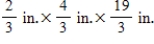B) 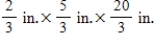C) ​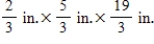 D) ​ E) ​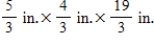

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: Find the relative extrema, if any, of

Q5: In the diagram, S represents the position

Q6: Determine where the function is concave upward

Q7: The owner of the Rancho Los Feliz

Q8: Find the graph of the derivative of

Q10: Select the graph of the function using

Q11: Determine where the function is concave downward.

Q12: The total annual revenue R of the

Q13: You are given the graph of some

Q14: Show that the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Show