Short Answer
A tomato is thrown from the top of a tomato cart its distance from the ground, in feet, is modeled by the equation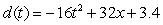 
where t is measured in seconds and the initial height of the cart is 
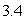feet.
(A) At what time is the tomato at its maximum height?
(B) What is the maximum height?
(C) What is the initial velocity of the tomato (at t = 0)?
Correct Answer:
Verified
Part A: 
...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q135: The derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="The derivative
Q136: The height off the ground of a
Q137: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="Find if
Q138: The concentration, in <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="The concentration,
Q139: The first derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="The
Q141: Differentiate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="Differentiate .
Q142: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg" alt="Find if
Q143: The amount, W, of fuel used by
Q144: Find the first derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8190/.jpg"
Q145: Find the first derivative of w(x) =