Multiple Choice
The centers of two slits of width a are a distance d apart. If the fourth minimum of the interference pattern occurs at the location of the first minimum of the diffraction pattern for light of wavelength λ, the ratio a/d is equal to
A) 0.
B) 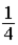 .
.
C) 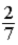 .
.
D) 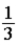 .
.
E)  .
.
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q37: Light from a helium-neon laser (λ =
Q38: When you look at a single slit
Q39: What, approximately, are the dimensions of the
Q40: White light is spread out into spectral
Q41: Unpolarized light is passed through three successive
Q42: When you look at a single slit
Q43: The large space telescope that has been
Q44: How wide must a narrow slit be
Q46: Helium-neon laser light (λ = 6.33 ×
Q47: Each pattern shown below would appear on