Solved

Scalar (Dot) Product: Determine the Scalar Product of =

Question 37

Multiple Choice

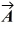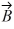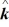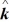
Scalar (dot) product: Determine the scalar product of Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined = 6.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined + 4.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined - 2.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined and Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined = 5.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined - 6.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined - 3.0 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined .


A) 30 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined + 24
Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined + 6
Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined
B) 30 Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined - 24
Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined + 6
Scalar (dot) product: Determine the scalar product of = 6.0 + 4.0 - 2.0 and = 5.0 - 6.0 - 3.0 . A) 30 + 24 + 6 B) 30 - 24 + 6 C) 12 D) 60 E) undefined
C) 12
D) 60
E) undefined

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q32: Components: The magnitude of a vector can

Q33: Components: The components of vector <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8274/.jpg"

Q34: Unit vectors: Vector <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8274/.jpg" alt="Unit vectors:

Q35: Scalar (dot) product: The value of the

Q36: Unit vectors: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8274/.jpg" alt="Unit vectors:

Q38: Scalar (dot) product: If two nonzero vectors

Q39: Components: As shown in the figure, three

Q40: Vector (cross) product: What is the vector

Q41: Components: Which of the following is an

Q42: Addition and subtraction: You walk 53 m