Two Different Workbooks and Two Distinct Teaching Machines Were to Be

Short Answer

Two different workbooks and two distinct teaching machines were to be evaluated on their effectiveness in teaching the concept of multiplication. A fourth grade class of 24 subjects was randomly assigned to 4 groups and each group in turn was randomly assigned to a teaching method. A test was given and the number of errors was recorded. This problem uses the Kruskal-Wallis H test to see if the number of errors differs from one teaching method to another. 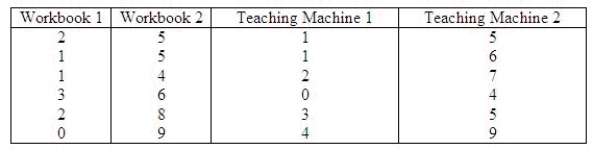What is the value of H in this problem?
______________
Find the rejection region for 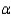= 0.05.
Reject 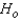if H > ______________
Conclude: ______________
There is ______________ evidence at 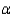= 0.05 to say that the number of errors differs from one teaching method to another.
What is the p-value for this test?
______________