Essay
Americans are very vocal about their attempts to improve personal well-being by "eating right and exercising more." One desirable dietary change is to reduce the intake of red meat and to substitute poultry or fish. A medical team from Florida tracked beef and chicken consumption (in annual pounds per person) and found the consumption of beef declining and the consumption of chicken increasing from 1970 through the year 2000. A summary of their data is shown in the table.
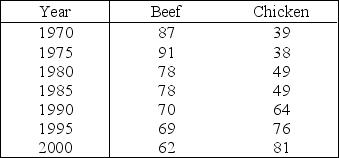 Consider fitting the following model, which allows for simultaneously fitting two simple linear regression lines: E(y) = 0+ 1x1 + 2x2+ 3x1x2 where
Consider fitting the following model, which allows for simultaneously fitting two simple linear regression lines: E(y) = 0+ 1x1 + 2x2+ 3x1x2 where 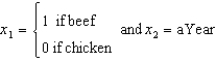 Minitab printouts using this model are provided here.
Minitab printouts using this model are provided here.
Regression Analysis
The regression equation is
Y = -3020 + 4897 X1 + 1.55 X2 - 2.46 X1X2

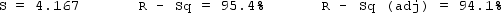 Analysis of Variance
Analysis of Variance

 Predicted Value
Predicted Value
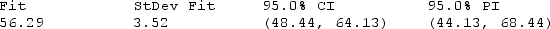
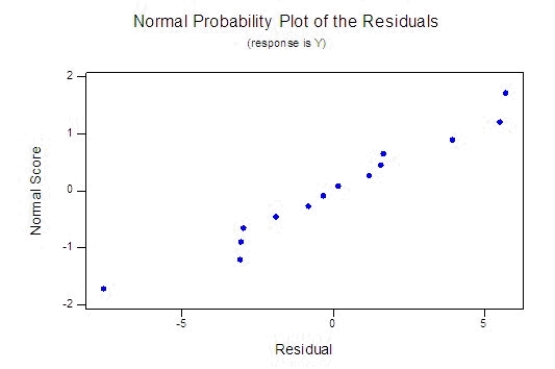
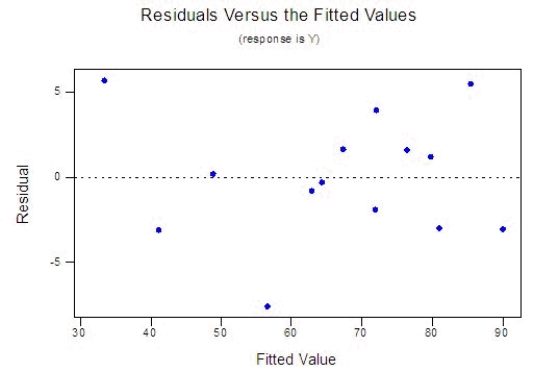 How well does the model fit? Use any relevant statistics and diagnostic tools from the printout to answer this question.
How well does the model fit? Use any relevant statistics and diagnostic tools from the printout to answer this question.
Test statistic:
F = ______________
p-value: ______________
Conclude:
The model ______________ significant information for the prediction of y.
Write the equations of the two straight lines that describe the trend in consumption over the period of 30 years for beef and for chicken.
For chicken: 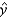 = _______ + _______
= _______ + _______ 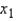 For beef:
For beef: 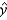 = _______ + _______
= _______ + _______ 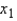 Use the prediction equation to find a point estimate of the average per-person beef consumption in 2005.
Use the prediction equation to find a point estimate of the average per-person beef consumption in 2005. 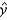 = ______________
= ______________
Compare this value with the value labeled "Fit" in the printout.
______________
Use the printout to find a 95% confidence interval for the average per-person beef consumption in 2005.
The confidence interval is:
CI = ______________ Enter (n1, n2)
What is the 95% prediction interval for the per-person beef consumption in 2005?
The 95% prediction interval is:
PI = ______________ Enter (n1, n2)
Is there any problem with the validity of the 95% confidence level for these intervals?
__________________________________________
Correct Answer:

Verified
69.83; 0; contributes; -3022.2; 1.55; 18...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q17: Which of the following statements is true?<br>A)
Q18: In testing the validity of a multiple
Q19: An engineer was investigating the relationship between
Q20: In a multiple regression analysis, if the
Q21: A chemist was interested in examining the
Q23: The computer output for a multiple regression
Q24: The adjusted coefficient of determination is adjusted
Q25: In reference to the equation: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8220/.jpg"
Q26: A multiple regression model involves 3 predictor
Q27: The coefficient of determination R<sup>2</sup> represents the