A Customer Service Representative Was Interested in Comparing the Average

Short Answer

A customer service representative was interested in comparing the average time (in minutes) customers are placed on hold when calling Southern California Edison and Southern California Gas companies. The representative obtained two independent random samples and calculated the following summary information: Assume the distributions of time a customer is on hold are approximately normal. Is it reasonable to assume equality of variances in this problem? Test whether there is a significant difference in average time a customer is on hold between the two companies.
Calculate the value of the test statistic. Set up the appropriate rejection region for the test in part (a) assuming 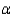= 0.10.
What is the appropriate conclusion?
Test Statistic = ______________
Reject Region: Reject H₀ if |t| > ______________
Conclusion: ______________
One ______________ conclude that there is a significant difference in mean time a customer is on hold between the two companies.