Solved

Assume That Two Independent Random Samples of Sizes and

Question 113

True/False

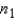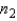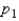Assume that two independent random samples of sizes Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and , respectively. The standard error of the sampling distribution of , the difference between sample proportions, is estimated by . and Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and , respectively. The standard error of the sampling distribution of , the difference between sample proportions, is estimated by . have been selected from binomial populations with parameters Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and , respectively. The standard error of the sampling distribution of , the difference between sample proportions, is estimated by . and Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and , respectively. The standard error of the sampling distribution of , the difference between sample proportions, is estimated by . , respectively. The standard error of the sampling distribution of Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and , respectively. The standard error of the sampling distribution of , the difference between sample proportions, is estimated by . , the difference between sample proportions, is estimated by Assume that two independent random samples of sizes and have been selected from binomial populations with parameters and 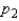, respectively. The standard error of the sampling distribution of 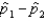, the difference between sample proportions, is estimated by . .

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q108: A questionnaire is designed to investigate attitudes

Q109: A 95% lower confidence bound (LCB) for

Q110: An unbiased estimator of a population parameter

Q111: A sample statistic such that the mean

Q112: The term confidence level refers to:<br>A) the

Q114: A random sample of 80 jars of

Q115: A comparison between the average jail time

Q116: The Postmaster at the Harrington Post Office

Q117: Suppose you wish to estimate a population

Q118: A random sample of 45 door-to-door encyclopedia