The Proportion of Individuals with an Rh-Positive Blood Type Is

Short Answer

The proportion of individuals with an Rh-positive blood type is 88%. You have a random sample of n = 500 individuals.
What is the mean of 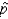, the sample proportion with Rh-positive blood type?
______________
What is the standard deviation?
______________
Is the distribution approximately normal?
______________
What is the probability that the sample proportion exceeds 85%.
______________
What is the probability that the sample proportion 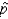lies between 86% and 91%?
______________
99% of the time, the sample proportion 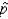would lie between what two limits?
Lower Limit = ______________
Upper Limit = ______________