Solved

If X Is a Normal Random Variable with Mean

Question 137

True/False

If x is a normal random variable with mean If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 4 and standard deviation If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 2, and Y is a normal random variable with mean If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 10 and standard deviation If x is a normal random variable with mean 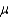= 4 and standard deviation 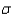= 2, and Y is a normal random variable with mean 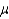= 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 5, then P(x < 0) = P(Y < 0).

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q132: The normal random variable's density function is

Q133: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8220/.jpg" alt="Let be

Q134: One difference between a binomial random variable

Q135: Which of the following is not a

Q136: For a continuous random variable, P(x <img

Q138: A chemical manufacturer sells its product in

Q139: Using the standard normal curve, the z-score

Q140: Twenty-five psychology instructors have formed a committee

Q141: The mean of any normal distribution is

Q142: Using the standard normal curve, the z-score