Solved

A Random Variable X Is Normally Distributed with M =

Question 130

Short Answer

A random variable x is normally distributed with m = 100 and 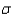A random variable x is normally distributed with m = 100 and = 20. What is the median of this distribution? ______________ Find . ______________ Find . ______________ = 20.
What is the median of this distribution?
______________
Find A random variable x is normally distributed with m = 100 and = 20. What is the median of this distribution? ______________ Find . ______________ Find . ______________ .
______________
Find A random variable x is normally distributed with m = 100 and = 20. What is the median of this distribution? ______________ Find 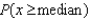. ______________ Find . ______________ .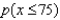
______________

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q125: Many different types of continuous random variables

Q126: Given a normal random variable x with

Q127: A car dealership has found that the

Q128: Using the standard normal curve, the area

Q129: The z-score representing the first quartile of

Q131: Given that Z is a standard normal

Q132: The normal random variable's density function is

Q133: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8220/.jpg" alt="Let be

Q134: One difference between a binomial random variable

Q135: Which of the following is not a