Restaurateur Denny Valentine Is Evaluating Two Sites, Raymondville and Rosenberg $\sigma$

Multiple Choice

Restaurateur Denny Valentine is evaluating two sites, Raymondville and Rosenberg, for his next restaurant.He wants to prove that Raymondville residents (population 1) dine out more often than Rosenberg residents (population 2) .Denny commissions a market survey to test this hypothesis.The market researcher used a random sample of 64 families from each suburb, and reported the following: 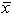₁ = 15 times per month and 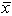₂ = 14 times per month.Assume that $\sigma$ ₁ = 2 and $\sigma$ ₂ = 3.With $\alpha$ = .01, the critical z value is ___.

A) -1.96
B) 1.96
C) -2.33
D) -1.33
E) 2.33