Solved

Determine the Values of X for Which the Function

Question 59

Multiple Choice

Determine the values of x for which the function Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E) can be replaced by the Taylor polynomial Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E) if the error cannot exceed 0.006. Round your answer to four decimal places.


A) Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E)
B) Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E)
C) Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E)
D) Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.006. Round your answer to four decimal places. A) B) C) D) E)
E) Determine the values of x for which the function 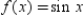can be replaced by the Taylor polynomial 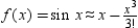if the error cannot exceed 0.006. Round your answer to four decimal places. A) 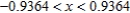B) 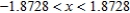C) D) 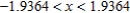E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q54: Determine the convergence or divergence of the

Q55: Suppose the winner of a $10,000,000 sweepstakes

Q56: Use Theorem 9.11 to determine the convergence

Q57: Use the Limit Comparison Test (if possible)

Q58: Determine the convergence or divergence of the

Q60: Determine whether the series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Determine

Q61: Suppose the annual spending by tourists in

Q62: Use the Direct Comparison Test to determine

Q63: Find the sum of the convergent series

Q64: Use the Root Test to determine the