Solved

Find a Geometric Power Series for the Function Centered at 0

Question 147

Multiple Choice

Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. A) B) C) D) E)


A) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. A) B) C) D) E)
B) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. A) B) C) D) E)
C) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. A) B) C) D) E)
D) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. A) B) C) D) E)
E) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. 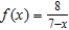A) 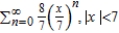B) 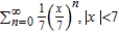C) D) 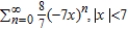E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q142: Find the positive values of p for

Q143: Use the Integral Test to determine the

Q144: A government program that currently costs taxpayers

Q145: Use the binomial series to find the

Q146: Identify the most appropriate test to be

Q148: Find the Maclaurin polynomial of degree 5

Q149: Use the Limit Comparison Test to determine

Q150: Write the first three terms of the

Q151: The terms of a series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q152: Use the Limit Comparison Test (if possible)