Solved

Find the Smallest N Such That the Error Estimate in the Approximation

Question 35

Multiple Choice

Find the smallest n such that the error estimate in the approximation of the definite integral 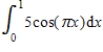is less than 0.00001 using Simpson's Rule.

A) 65
B) 10
C) 13
D) 18
E) 23

Related Questions

Q30: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find .

Q31: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q32: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q33: Find the smallest n such that the

Q34: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q36: A hydraulic cylinder on an industrial machine

Q37: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q38: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q39: Use the error formula to estimate the

Q40: Determine whether the improper integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"