Solved

Find the Smallest N Such That the Error Estimate from the Error

Question 124

Multiple Choice

Find the smallest n such that the error estimate from the error formula in the approximation of the definite integral Find the smallest n such that the error estimate from the error formula in the approximation of the definite integral 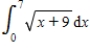is less than 0.00001 using the Trapezoidal Rule. ​ A) 282 B) 66 C) 749 D) 163 E) 24 is less than 0.00001 using the Trapezoidal Rule. ​


A) 282
B) 66
C) 749
D) 163
E) 24

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q119: Determine whether the improper integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q120: Suppose a damping force affects the vibration

Q121: Find the indefinite integral by making the

Q122: Find the indefinite integral by making the

Q123: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Evaluate .

Q125: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q126: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find .

Q127: Use integration tables to find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q128: Determine whether the improper integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q129: Use partial fractions to find the integral