Solved

The Logistic Function Models the Growth of a Population

Question 46

Multiple Choice

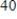The logistic function The logistic function models the growth of a population. Determine when the population reaches % of the maximum carrying capacity. Round your answer to three decimal places. A) 4.317 B) 3.000 C) 0.474 D) 0.677 E) 0.301 models the growth of a population. Determine when the population reaches The logistic function models the growth of a population. Determine when the population reaches % of the maximum carrying capacity. Round your answer to three decimal places. A) 4.317 B) 3.000 C) 0.474 D) 0.677 E) 0.301 % of the maximum carrying capacity. Round your answer to three decimal places.


A) 4.317
B) 3.000
C) 0.474
D) 0.677
E) 0.301

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q41: Find an equation of the graph that

Q42: Suppose that the population (in millions) of

Q43: Sketch the slope field for the differential

Q44: Match the logistic equation with its graph.

Q45: Solve the differential equation. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q47: Suppose that the population (in millions) of

Q48: Use the differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Use

Q49: The isotope <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="The isotope

Q50: A phase trajectory is shown for populations

Q51: Solve the first order linear differential equation.